Video: Is Pi 'n polinoom?
2024 Outeur: Lynn Donovan | [email protected]. Laas verander: 2023-12-15 23:42
PI (π) word nie as 'n beskou nie polinoom . Dit is 'n waarde wat verwys na die omtrek van 'n sirkel. Aan die ander kant, polinoom verwys na 'n vergelyking wat vier veranderlikes of meer bevat.
Hiervan, kan pi deel van 'n polinoom wees?
Die antwoord is NEE. As daar 'n polinoom met algebraïese koëffisiënte, sal daar ook 'n wees polinoom met rasionale koëffisiënt (met 'n groter graad). Dit is omdat ˉQ algebraïes gesluit is. Veronderstel dat π was die wortel van 'n polinoom f(x)=xn+an−1xn−1+⋯+a0 met die ai as algebraïese getalle.
Tweedens, wat maak 'n polinoom? In wiskunde, a polinoom is 'n uitdrukking wat bestaan uit veranderlikes (ook genoem onbepaalde) en koëffisiënte, wat slegs die bewerkings van optel, aftrek, vermenigvuldiging en nie-negatiewe heelgetal eksponente van veranderlikes behels. 'n Voorbeeld van 'n polinoom van 'n enkele onbepaalde, x, is x2 − 4x + 7.
In hierdie verband, is Pi 'n Monomiaal?
Ja, π π is a monomiaal want dit is 'n nommer.
Moet 'n polinoom 'n veranderlike hê?
Dus: A polinoom kan het konstantes, veranderlikes en eksponente, maar nooit deling deur a nie veranderlike . Hulle kan ook het een of meer terme, maar nie 'n oneindige aantal terme nie.
Aanbeveel:
Wat noem jy 'n polinoom met 6 terme?
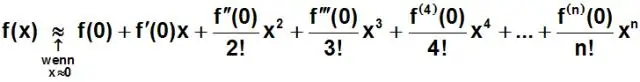
Die volgende name word volgens hul graad aan polinome toegeken: Graad 4 – kwarties (of, as alle terme ewe graad het, tweekwadraties) Graad 5 – kwinties. Graad 6 - seksties (of, minder algemeen, heksies)
Wat is 'n eerstegraadse polinoom?
Eerstegraadse polinome. Eerstegraadse polinome staan ook bekend as lineêre polinome. In die besonder, eerstegraadse polinome is lyne wat nie horisontaal of vertikaal is nie. Letter m word meer dikwels gebruik as die koëffisiënt van x in plaas van a, en word gebruik om die helling van die lyn voor te stel
Wat is 3de graad polinoom?
Derdegraadse polinome staan ook bekend as kubieke polinome. Kubieke het hierdie eienskappe: Een tot drie wortels. Twee of nul ekstrema. Wortels is oplosbaar deur radikale
Wat is 'n ekwivalente polinoom?
Daarbenewens is twee polinome ekwivalent as al die koëffisiënte van een 'n konstante (nie-nul) veelvoud van die ooreenstemmende koëffisiënte van die ander is
Is die som van twee polinome altyd 'n polinoom?
Die som van twee polinome is altyd 'n polinoom, so die verskil van twee polinome is ook altyd 'n polinoom