
- Outeur Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:42.
- Laas verander 2025-01-22 17:14.
Die groot O van 'n lus is die aantal iterasies van die lus in aantal stellings binne die lus . Nou volgens die definisie, die Groot O moet wees O (n*2) maar dit is O (n).
Net so kan jy vra, wat is die kompleksiteit van 'n for-lus?
Aangesien ons aanneem die stellings is O(1), is die totale tyd vir die for lus is N * O(1), wat in die geheel O(N) is. Die buitenste lus voer N keer uit. Elke keer die uiterlike lus voer, die innerlike lus voer M keer uit. As gevolg hiervan, die stellings in die innerlike lus voer 'n totaal van N * M keer uit.
Verder, wat is Big O-notasie met voorbeeld? Die Groot O-notasie definieer 'n boonste grens van 'n algoritme, dit beperk 'n funksie slegs van bo af. Vir voorbeeld , oorweeg die geval van Invoegingssorteer. Dit neem lineêre tyd in beste geval en kwadratiese tyd in slegste geval. Ons kan met sekerheid sê dat die tydskompleksiteit van Invoegingssoort is O (n^2).
Eenvoudig so, hoe vind jy die tydskompleksiteit van 'n for-lus?
Byvoorbeeld Seleksie sorteer en Invoeg sorteer het O(n^2) tyd kompleksiteit . O (Aanmeld) Tydskompleksiteit van 'n lus word as O(Logn) beskou as die lus veranderlikes word gedeel / vermenigvuldig met 'n konstante bedrag. Binêre soektog het byvoorbeeld O(Logn) tyd kompleksiteit.
Hoe bereken jy Big O?
Om bereken Groot O , kan jy deur elke reël kode gaan en vasstel of dit is O (1), O (n) ens en gee dan jou terug berekening aan die einde. Dit kan byvoorbeeld wees O (4 + 5n) waar die 4 vier gevalle van verteenwoordig O (1) en 5n verteenwoordig vyf gevalle van O (n).
Aanbeveel:
Wat is die beste gratis sagteware vir die verwydering van virusse vir Windows 7?
Bitdefender Antivirus Free Edition. Diskrete maar effektiewe, Bitdefender is die beste anti-wanware vir jou rekenaar. Avira Free Security Suite. Avira FreeAntivirus. AVG AntiVirus Gratis. Malwarebytes Anti-Malware. SpyBot Soek & Vernietig. Emsisoft Emergency Kit. Avast anti-virus
Wat is die frekwensie van vrystelling van groot innovasies vir S 4hana Cloud Edition?
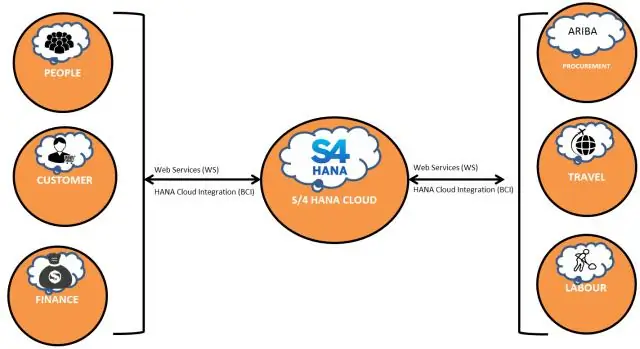
S/4HANA-weergawe op die perseel het 'n jaarlikse groot vrystelling wat laas 1709 is (in September 2017) en die volgende een wat in 1809 (September 2018) beplan word. Gedurende die jaar stel SAP ook die 2 FPS (Functional Pack Stacks) vry wat niks anders is as om die vereenvoudigings van wolkweergawe na plaaslike weergawe af te dra nie
Wat is die straf in Indië vir die steel van rekenaardokumentebates of enige sagteware se bronkode van enige organisasie individu of van enige ander manier?

Verduideliking: Die straf in Indië vir die steel van rekenaardokumente, bates of enige sagteware se bronkode van enige organisasie, individu of van enige ander manier is 3 jaar gevangenisstraf en 'n boete van Rs. 500 000
Wat is die nutsmiddels vir die opsporing van defekte wat vir mobiele toetse gebruik word?
Daar is baie gereedskap beskikbaar vir defektopsporing. Die volgende is die defekopsporingsgereedskap wat vir mobiele toetse gebruik word: Airbrake Bug Tracker. Mantis. Bugzilla. JIRA. Zoho Bug Tracker. FogBugz. Vuurtoring. Trac
Wat is die beste manier vir die toepassing om die groot lêers in s3 op te laai?
Die grootste enkele lêer wat in 'n Amazon S3-emmer in 'n enkele PUT-bewerking opgelaai kan word, is 5 GB. As jy groot voorwerpe (> 5 GB) wil oplaai, sal jy dit oorweeg om meervoudige oplaai-API te gebruik, wat dit moontlik maak om voorwerpe van 5 MB tot 5 TB op te laai
