Video: Wat is die kompleksiteit van hoop sorteer algoritme?
2024 Outeur: Lynn Donovan | [email protected]. Laas verander: 2023-12-15 23:42
Hoopsortering is 'n in-plek algoritme. TydKompleksiteit : Tyd kompleksiteit van heapify is O(Logn). Tyd kompleksiteit van createAndBuildHeap() is O(n) en algehele tyd kompleksiteit van Hoop Sorteer is O(nLogn).
Met betrekking tot hierdie, wat is die algoritme van hoopsoort?
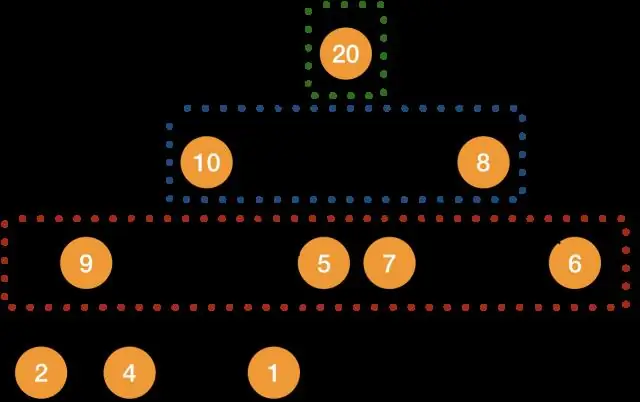
Hoop sorteer algoritme word in twee basiese dele verdeel: Die skep van a Hoop van die ongesorteerde lys/skikking. Toe a gesorteer skikking word geskep deur herhaaldelik die grootste/kleinste element uit die hoop , en plaas dit in die skikking. Die hoop word na elke verwydering gerekonstrueer.
Net so, wat is die tipiese looptyd van 'n hoopsoortalgoritme? Quicksort het egter 'n ergste geval looptyd van O (n 2) O(n^2) O(n2) en 'n slegste-geval spasie kompleksiteit van O (log ? n O(log n O(logn), so as dit baie belangrik is om 'n vinnige ergste-geval te hê looptyd en doeltreffende ruimtegebruik, hoopsoort is die beste opsie.
Net so word gevra, wat is die kompleksiteit van Heapify-funksie?
Die hoofgedagte is dat in die build_heap algoritme die werklike ophoop koste is nie O(log n) vir alle elemente nie. Wanneer ophoop genoem word, hang die looptyd af van hoe faran-element in die boom kan afbeweeg voordat die proses eindig. Met ander woorde, dit hang af van die hoogte van die element in die hoop.
Watter sorteeralgoritme het die beste asimptotiese kompleksiteit?
Vir Beste geval Invoeging Sorteer en Hoop Sorteer is die beste een as hulle beste saak loop tyd kompleksiteit is O(n). Vir gemiddelde geval beste asimptotiese hardloop tyd kompleksiteit is O(nlogn) wat deur Merge gegee word Sorteer , Hoop Sorteer , Vinnig Sorteer . Vir die ergste geval beste hardloop tyd kompleksiteit is O(nlogn) wat gegee word deur Merge Sorteer , Hoop Sorteer.
Aanbeveel:
Watter sorteeralgoritme het die beste asimptotiese kompleksiteit?
Hoop Sorteer
Waar is die hoop in 'n masjien se geheuekaart geleë?
By die hoër adresse is die stapel en by die laer adres is die hoop. Die twee geheue-toewysingsstreke groei in die middel van die adresruimte, wat ongebruik en ongeallokeerd is
Word gedefinieer as die verband tussen eienskappe van 'n voorwerp en die vermoëns van 'n agent wat leidrade verskaf tot die gebruik van 'n voorwerp?
'n Bekostiging is 'n verhouding tussen die eienskappe van 'n voorwerp en die vermoëns van die agent wat bepaal presies hoe die voorwerp moontlik gebruik kan word
Wat is die kompleksiteit van Dijkstra se algoritme?
Tydkompleksiteit van Dijkstra se algoritme is O (V 2), maar met min-prioriteit-tou val dit af na O (V + E l o g V)
Wat is die beste geval tyd kompleksiteit van samesmelting soort?
Sorteeralgoritmes Algoritme Datastruktuur Ruimtekompleksiteit:Slegste Vinnige sorteer Skikking O(n) Voeg saam sorteer Skikking O(n) Hoopsortering Skikking O(1) Gladde sorteer Skikking O(1)