Video: Waarom is trigonometriese identiteite nuttig om vergelykings op te los?
2024 Outeur: Lynn Donovan | [email protected]. Laas verander: 2023-12-15 23:42
Identiteite stel ons in staat om ingewikkelde uitdrukkings te vereenvoudig. Hulle is die basiese gereedskap van trigonometrie wat gebruik word om trigonometriese vergelykings op te los , net soos faktorisering, vind van gemene delers en die gebruik van spesiale formules die basiese gereedskap van oplos algebraïes vergelykings.
Wat maak dan 'n trigonometriese vergelyking 'n identiteit?
In wiskunde, trigonometriese identiteite is gelykhede wat behels trigonometriese funksies en is waar vir elke waarde van die verskynende veranderlikes waar beide kante van die gelykheid gedefinieer is. Geometries is dit identiteite wat sekere funksies van een of meer hoeke behels.
Weet ook, wat is trigonometriese vergelykings? A trigonometriese vergelyking is enige vergelyking wat 'n bevat trigonometriese funksie. Soos genoem in Trigonometries Identiteite, a trigonometriese vergelyking wat geld vir enige hoek word a genoem trigonometriese identiteit. Daar is ander vergelykings , dit is egter net waar vir sekere hoeke.
Net so kan 'n mens vra, wat is die maklikste manier om trigonometriese identiteite op te los?
STAP 1: Skakel alle sec, csc, cot en tan om na sin en cos. Die meeste hiervan kan gedoen word deur die kwosiënt en wederkerig te gebruik identiteite . STAP 2: Kontroleer al die hoeke vir somme en verskille en gebruik die toepaslike identiteite om hulle te verwyder. STAP 3: Kyk vir hoekveelvoude en verwyder dit deur die toepaslike formules te gebruik.
Wat is sonde 2x gelyk?
sonde 2x =( sonde x)2=12(1−cos( 2x )).
Aanbeveel:
Hoekom is gevaldiagramme nuttig?
Wanneer Unified Modeling Language (UML) gebruik word, help 'n gebruiksgevaldiagram jou om te verstaan hoe 'n gebruiker interaksie kan hê met die stelsel wat jy ontwerp het. En op die ou end behoort dit jou span te help om vereistes te definieer en te organiseer. In plaas daarvan verteenwoordig hulle 'n hoëvlakoorsig van hoe gebruiksgevalle, akteurs en jou stelsel verband hou
Waarom is Schottky-diode nuttig vir hoëfrekwensie-regstelling?
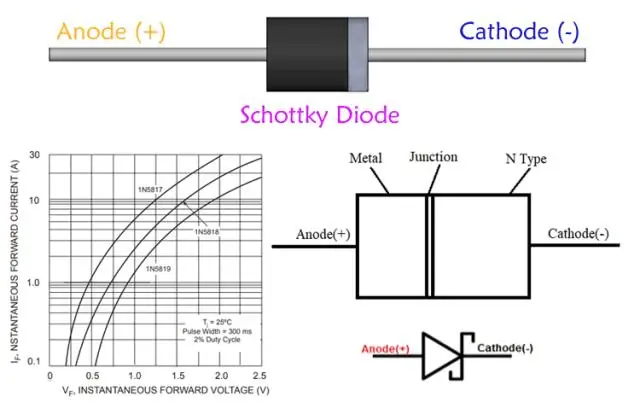
Schottky diode toepassings. Kraggelykrigter: Schottky-diodes word ook as hoëkrag-gelykrigters gebruik. Hul hoë stroomdigtheid en lae voorwaartse spanningsval beteken dat minder krag vermors word as wanneer gewone PN-aansluitingsdiodes gebruik word. Schottkydiodes is geneig om 'n hoë omgekeerde lekstroom te hê
Hoe is Six Sigma nuttig?
Six Sigma is 'n stel gereedskap en tegnieke wat deur maatskappye gebruik word om produksieprosesse te verbeter, defekte uit te skakel en kwaliteit te waarborg. Die Six Sigma-sertifisering help met die validering van professionele persone wat vaardig is om risiko's, foute of defekte in 'n besigheidsproses te identifiseer en dit te verwyder
Hoe los jy vergelykings in Mathcad op?
Om vergelykings simbolies op te los. Tik die vergelyking om op te los deur die Booleaanse gelyk aan operateur te gebruik. Voeg die simboliese evaluasie-operateur in, tik die sleutelwoord oplos in die plekhouer, en druk dan Enter of klik enige plek. PTC Mathcad gee simboliese oplossings vir die vergelyking, indien moontlik
Waarom is kundige resensies nuttig?
Kundige resensies is 'n tegniek wat deur UX-navorsers gebruik word om die bruikbaarheid van 'n webwerf of ander digitale produk te evalueer. Uiteindelik moet albei tegnieke lei tot 'n stel geprioritiseerde aanbevelings vir die verbetering van die bruikbaarheid en gebruikerservaring van u webwerf