Watter vorms kan nie tesseleer nie?

Video: Watter vorms kan nie tesseleer nie?

2024 Outeur: Lynn Donovan | [email protected]. Laas verander: 2023-12-15 23:42

Onder gereelde veelhoeke, 'n reëlmatige seshoek willtessellate, soos 'n gereelde driehoek en 'n gereelde vierhoek ( Vierkantig ). Maar geen ander nie gereelde veelhoek sal tesseleer.

Op hierdie manier, watter vorms kan jy tesseleer?

Driehoeke, vierkante en seshoeke is die enigste reëlmatige vorms watter tesseleer by hulself. Jy kan ander het tessellasies van gereelde vorms as jy gebruik meer as een soort vorm . Jy kan selfs tesseleer vyfhoeke, maar hulle sal nie gereelde wees nie. Tessellasies kan word gebruik vir teëlpatrone of in lappieskomberse!

Ook, watter veelhoek sal nie 'n vliegtuig tesseleer nie? 2. Watter gereelde veelhoeke sal tesseleer op hul eie sonder enige spasies of oorvleuelings? Gelyksydige driehoeke, vierkante en reëlmatige seshoeke is die enigste gereelde veelhoeke daardie sal tesseleer . Daarom, daar is slegs drie gereelde tessellasies.

Om ook te weet, is watter vorm nie gebruik kan word om 'n gereelde tessellasie te maak nie?

Daar is net drie vorms wat so kan vorm gereelde tesellasies : die gelyksydige driehoek, vierkant, en gereelde seshoek. Enige een van hierdie drie vorms kan oneindig gedupliseer word om 'n vliegtuig met geen gapings te vul nie. Baie ander tipes tessellasie is moontlik onder verskillende beperkings.

Hoe bepaal jy of 'n vorm kan tesseleer?

As die figuur is aan alle kante dieselfde, dit sal pas bymekaar wanneer dit herhaal word. Syfers wat tesseleer is geneig om gereelde veelhoeke te wees. Gereelde veelhoekskeer kongruente reguit sye. Wanneer jy 'n gewone veelhoek draai of skuif, die kant van die oorspronklike figuur en die kant van sy vertaling sal pas.

Aanbeveel:

Watter karakters kan jy nie in 'n lêernaam gebruik nie?

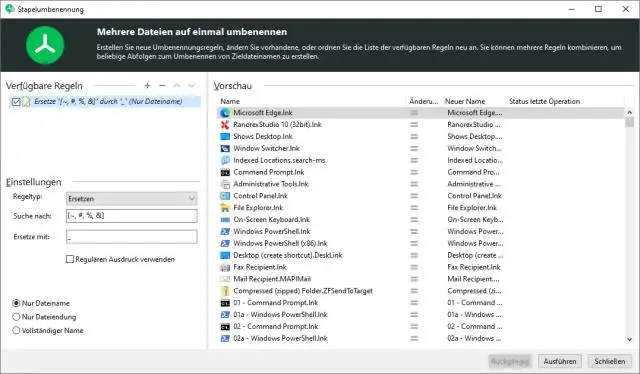
Jy kan nie die volgende karakters enige plek in 'n lêernaam gebruik nie: Tilde. Nommer teken. Persentasie. Ampersand. Asterisk. Draadjies. Terugskuinsstreep. Dubbelpunt

Kan nie aan bediener koppel nie. Nie so 'n lêer of gids PSQL nie?

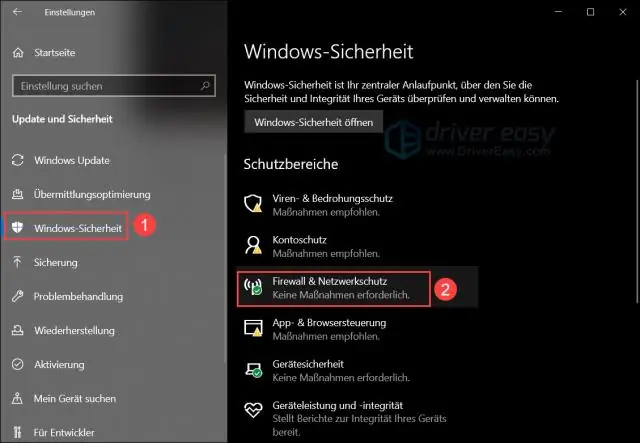
Psql: kon nie aan bediener koppel nie: Geen so 'n lêer of gids Werk die bediener plaaslik en aanvaar verbindings op Unix-domein-sok '/var/run/postgresql/. EDIT-opdragte wat ek gebruik het om postgres te installeer en uit te voer: sudo apt-get update. sudo apt-get installeer postgresql. sudo su postgres. psql -d postgres -U postgres

Kon nie koppel nie bediener loop dalk nie kan nie koppel aan MySQL bediener op 127.0 0.1 10061?

As die MySQL-bediener op Windows werk, kan jy met TCP/IP koppel. Jy moet ook seker maak dat die TCP/IP-poort wat jy gebruik nie deur 'n firewall of poortblokkeerdiens geblokkeer is nie. Die fout (2003) Kan nie aan MySQL-bediener koppel op 'bediener' (10061) dui aan dat die netwerkverbinding geweier is

Watter handelinge kan nie in Microsoft Word ontdoen word nie?

Woordles 1 Flitskaarte A B Watter van die volgende aksies of opdragte kan nie in Microsoft Word ongedaan gemaak word nie? Stoor 'n dokument Watter van die volgende versteekte formateringssimbool verteenwoordig 'n tabstop in 'n dokument? 'n Swart pyl wat regs wys Wat is die korrekte lêerformaat van 'n normale Microsoft Word-sjabloon?.dotx