Video: Is die twee hoeklyne van 'n parallelogram gelyk?
2024 Outeur: Lynn Donovan | [email protected]. Laas verander: 2023-12-15 23:42
Wanneer 'n parallelogram is verdeel in twee driehoeke kry ons om te sien dat die hoeke oor die gemeenskaplike sy(hier die diagonaal ) is gelyk . Dit bewys dat die teenoorgestelde hoeke in a parallelogram is ook gelyk . Die diagonale van 'n parallelogram is nie van nie gelyk lengte.
Net so, is diagonale van 'n parallelogram kongruent?
Al die eienskappe van 'n parallelogram toepas (die wat hier saak maak is parallelle sye, teenoorgestelde sye is kongruent , en diagonale verdeel mekaar). Alle hoeke is per definisie regte hoeke. Die diagonale is kongruent.
'n Mens kan ook vra, hoekom is die hoeklyne van 'n parallelogram nie kongruent nie? Die diagonale van 'n parallelogram is nie gelyk. Omdat die parallelogram het aangrensende hoeke as skerp en stomp, die diagonale verdeel die figuur in 2 pare van kongruent driehoeke. Aangesien die hoeke skerp of stomp is, is twee van die korter sye van die driehoeke, beide skerp en stomp, kongruent.
Net so, wat is die diagonaal van 'n parallelogram?
Diagonaal van Parallelogram Formule A parallelogram is 'n vierhoek waarvan die teenoorstaande sye ewewydig en gelyk is. Die teenoorgestelde sye wat ewewydig en gelyk is, vorm gelyke hoeke aan die teenoorgestelde sye. Diagonale van 'n parallelogram is die segmente wat die teenoorgestelde hoeke van die figuur verbind.
Is die twee hoeklyne van 'n reghoek gelyk Hoekom?
Die twee hoeklyne is kongruent (selfde lengte). Elkeen diagonaal halveer die ander. Met ander woorde, die punt waar die diagonale sny (kruis), verdeel elkeen diagonaal in twee gelyk dele. Elkeen diagonaal verdeel die reghoek in twee kongruente reghoekige driehoeke.
Aanbeveel:
Is hoeklyne van vierkant gelyk?
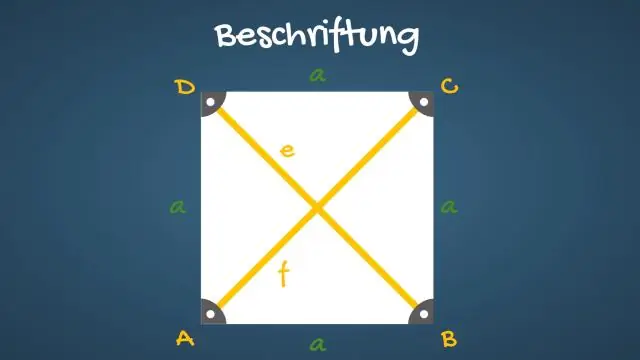
Die hoeklyne van 'n vierkant halveer sy hoeke. Teenoorstaande sye van 'n vierkant is ewe lank en ewe lank. Al vier sye van 'n vierkant is gelyk. Die hoeklyne van 'n vierkant is gelyk
Wat is twee voordele van die gebruik van LACP kies twee?
Wat is twee voordele van die gebruik van LACP? (Kies twee.) verhoog oortolligheid na Laag 3-toestelle. skakel die behoefte aan die spanning-tree protokol uit. laat outomatiese vorming van EtherChannel-skakels toe. bied 'n gesimuleerde omgewing vir die toets van skakelaggregasie
Is twee skikkings gelyk aan JavaScript?
In Javascript, om twee skikkings te vergelyk, moet ons seker maak dat die lengte van beide skikkings dieselfde moet wees, die voorwerpe wat daarin voorkom is van dieselfde tipe en elke item in een skikking is gelyk aan die eweknie in 'n ander skikking. Deur dit te doen kan ons aflei dat beide skikkings dieselfde is of nie. JavaScript bied 'n funksie JSON
Halveer hoeklyne mekaar altyd in 'n parallelogram?
In enige parallelogram halveer die hoeklyne (lyne wat teenoorstaande hoeke verbind) mekaar. Dit wil sê, elke diagonaal sny die ander in twee gelyke dele. Sleep enige hoekpunt in die figuur hierbo om die parallelogram te hervorm en oortuig jouself dat dit so is
Sal twee voorwerpe altyd gelyk wees wanneer hul vergelyk met () metode nul gee?
Dit word aanbeveel dat compareTo slegs 0 gee, as 'n oproep na gelyke op dieselfde voorwerpe waar sou teruggee: compareTo(e2) == 0 het dieselfde booleaanse waarde as e1. is gelyk aan (e2) vir elke e1 en e2 van klas C. Let daarop dat nul nie 'n geval van enige klas is nie, en e