Video: Hoe bewys jy dat die hoeklyne van 'n ruit mekaar halveer?
2024 Outeur: Lynn Donovan | [email protected]. Laas verander: 2023-12-15 23:42
In 'n ruit almal sye is gelyk en teenoorstaande sye is ewewydig. Verder a ruit is ook 'n parallelgram en vertoon dus eienskappe van a parallelogram en dit diagonale van 'n parallelogram halveer mekaar.
Dienooreenkomstig, halveer die hoeklyne van 'n ruit mekaar?
In enige ruit , die diagonale (lyne wat teenoorgestelde hoeke verbind) halveer mekaar reghoeke (90°). Dit wil sê, elke diagonaal sny die ander in twee gelyke dele, en die hoek waar hulle kruis is altyd 90 grade. In die figuur hierbo sleep enige hoekpunt om die te hervorm ruit en oortuig jouself dat dit so is.
Tweedens, is ruithoeklyne loodreg? Eienskappe van 'n Ruit Die diagonale is loodreg aan en halveer mekaar. Aangrensende hoeke is aanvullend (bv. ∠A + ∠B = 180°). A ruit is 'n parallelogram wie se diagonale is loodreg aan mekaar.
As jy dit in ag neem, hoe bewys jy die hoeklyne van 'n ruit is loodregte middellyne?
Bewys dat die diagonale van 'n ruit is loodreg Voortsetting van hierbo bewys : Ooreenstemmende dele van kongruente driehoeke is kongruent, dus is al 4 hoeke (die in die middel) kongruent. Dit lei tot die feit dat hulle almal gelyk is aan 90 grade, en die diagonale is loodreg aan mekaar.
Is ruit 'n parallelogram?
DEFINISIE: A ruit is 'n parallelogram met vier kongruente sye. STELLING: As a parallelogram is 'n ruit , halveer elke diagonaal 'n paar teenoorstaande hoeke. STELLING Omgekeerd: As a parallelogram diagonale het wat 'n paar teenoorstaande hoeke halveer, is dit a ruit.
Aanbeveel:
Is hoeklyne van vierkant gelyk?
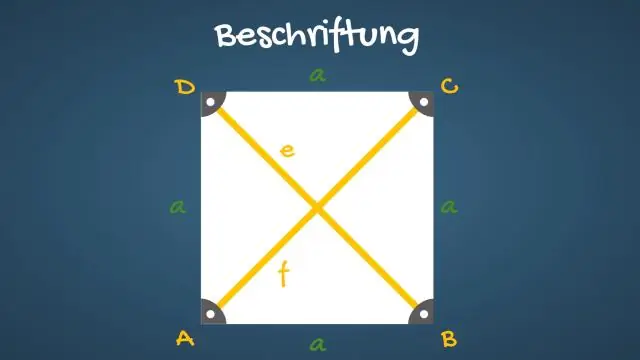
Die hoeklyne van 'n vierkant halveer sy hoeke. Teenoorstaande sye van 'n vierkant is ewe lank en ewe lank. Al vier sye van 'n vierkant is gelyk. Die hoeklyne van 'n vierkant is gelyk
Is die twee hoeklyne van 'n parallelogram gelyk?
Wanneer 'n parallelogram in twee driehoeke verdeel word, sien ons dat die hoeke oor die gemeenskaplike sy (hier die diagonaal) gelyk is. Dit bewys dat die teenoorgestelde hoeke in 'n parallelogram ook gelyk is. Die hoeklyne van 'n parallelogram is nie ewe lank nie
Halveer hoeklyne mekaar altyd in 'n parallelogram?
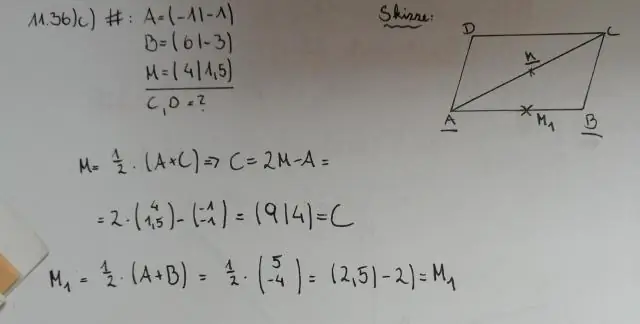
In enige parallelogram halveer die hoeklyne (lyne wat teenoorstaande hoeke verbind) mekaar. Dit wil sê, elke diagonaal sny die ander in twee gelyke dele. Sleep enige hoekpunt in die figuur hierbo om die parallelogram te hervorm en oortuig jouself dat dit so is
Halveer diagonale van parallelogram mekaar by 90?
In enige ruit halveer die hoeklyne (lyne wat teenoorstaande hoeke verbind) mekaar reghoekig (90°). Dit wil sê, elke diagonaal sny die ander in twee gelyke dele, en die hoek waar hulle kruis is altyd 90 grade
Watter parallelogramme het diagonale wat mekaar halveer?
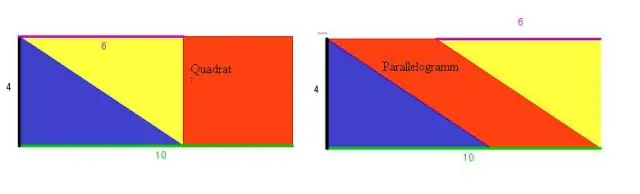
As twee aangrensende sye van 'n parallelogram gelyk is, dan is dit 'n ruit. Hierdie toets word dikwels as die definisie van 'n ruit geneem. 'n Vierhoek waarvan die hoeklyne mekaar reghoekig halveer, is 'n ruit